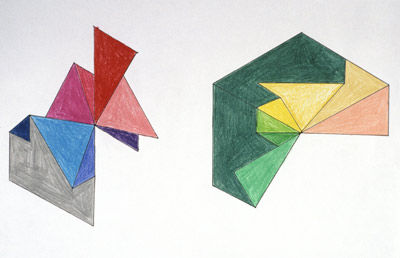Identical modules
The three modules are identical in surface area, volume, and orientation (symmetry). E.W.

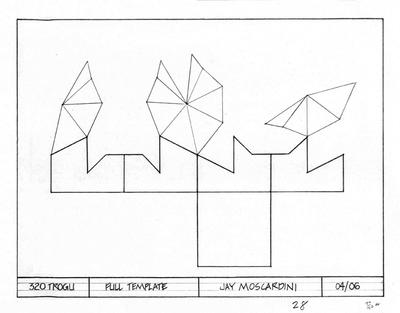
Cube module complete template.
The two colors differentiate the internal surface from the external. SFSU, E.W.

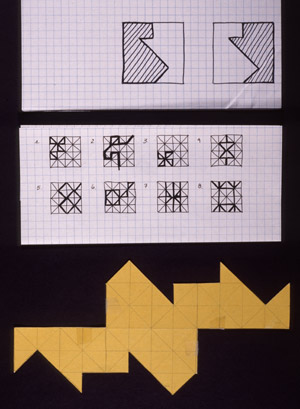
Basic sections of the square
The basic square grid determines what type of sections can be performed.

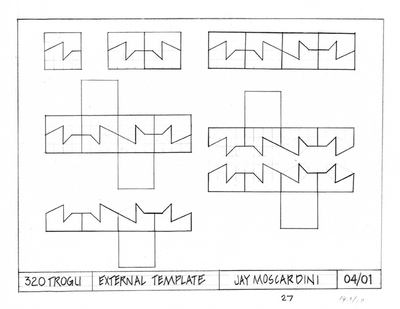
External fold-out surface - one module of three
Various sections of the face. Fold-out model of exterior surface of single module (1/3 of cubic volume.)
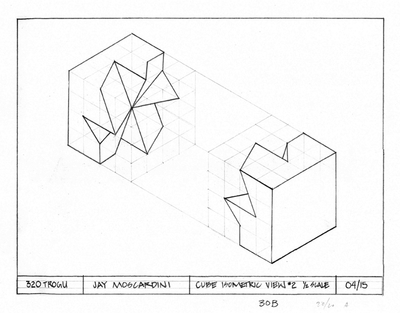
Cube - two parts (of three)
All surfaces of the cubic module, internal and external, are determined exactly by geometric construction, using compass, triangles, and ruler.

Cube 2-module process
Progressive sectioning and rotations of the modules on the plane. External surface. Drawing by Jay Moscardini - J.M.
12-module cube
A cube comprised of 12 identical modules. Closed state. Cube by Aliek Bertolucci - A.B., SFSU.

Cubic chain 1
Closed cubic chain composed of 24 modules (6 modules x 4 cubes), unfolded. Design by Florence Yuen. Instructor: Pino Trogu. San Francisco State University, Fall 2010.

Cube Section
Communication Vehicles I - Freshman Foundation, Virginia Commonwealth University - VCU and Drafting and Sketching for Design, San Francisco State UniversityIn this 3-D project, a square is first sectioned into two parts. The section is repeated on the six faces of the cube, which are then recombined to obtain more complex external surfaces. The external sections determine how the interior will be divided and a model is made, splitting the cube into three equal complex volumes. Based on the work of Paul Klee and Giorgio Scarpa. In some cases, a simpler cube can be made with only two modules. In a very complex case, 12 modules were used. In another variation, the modules in each cube can be linked to those in a another cube, forming open or closed chains that can be folded back into minimal cell volumes. An interesting question is whether such folding is always possible, regardless of the type of initial section of the cubic face. More information about the work of Giorgio Scarpa can be found at the URL below.
2014
res.trogu.com/scarpa/res.trogu.com/scarpa/